(1) (Всероссийская Олимпиада Школьников по информатике школьный уровень Московская область — 7-8 класс):(замечательная тройка)
Вчера Серёжа сказал Диме три целых положительных числа: a, b и c. Числа очень понравились Диме, поэтому он решил их записать, но особым образом, чтобы никто больше их не узнал. Дима выписал все попарные суммы и сумму всех трех чисел, то есть a + b, b + c, a + c и a + b + c. Для большей надежности он записал их в случайном порядке.
На следующий день Дима встретил Юлю и очень захотел всё-таки поделиться с ней этой замечательной тройкой чисел. К сожалению, за ночь он успел забыть, какие числа сказал ему Серёжа, поэтому теперь ему приходится восстанавливать числа по тому, что он записал. Напишите программу, которая по четырем записанным числам восстанавливает тройку чисел, которую Диме сказал Серёжа.
Формат входных данных
В четырех строках содержатся 4 целых числа: W; X; Y; Z (0 < W, X, Y, Z < 3001) – числа, которые записал Дима.
В первой строке W .
Во второй строке X.
В третьей строке Y .
В четвертой строке Z.
Формат выходных данных
Выведите 3 целых числа через пробел – тройку чисел, которую Диме сказал Сережа. Гарантируется, что существует хотя бы одна тройка чисел, удовлетворяющая требованиям. Если возможных ответов несколько, выведите любой.
Пример:

(2): (Всероссийская Олимпиада Школьников по информатике школьный уровень Московская область — 7-8 класс):(три числа)
Никита большой любитель чисел, поэтому недавно он придумал следующую игру. В начале Никита записывает три числа A, B и C. Далее эта тройка чисел преобразуется в тройку C — B, A и 2 * A. Такая операция повторяется K раз. Например, если изначально были выбраны A = 1, B = 2 и C = 5 и количество повторений
операции K = 2, то после первой операции будет получена тройка чисел A = 5 — 2 = 3, B = 1 и C = 2 * 1 = 2. После второй операции будет получена тройка чисел A = 2 — 1 = 1, B = 3 и C = 2 * 3= 6. Вам необходимо определить, какая тройка будет получена после K повторов операции над числами A, B и C.
Формат выходных данных
Введите три целых числа тройку чисел в той последовательности, в которой они получатся после применения K операций к исходным трем числам A, B и C.
Замечание:
Тест №1(задача B.1): A = 3, B = 5, C = 8, K = 2;
Тест №2(задача B.2): A = 6, B = 7, C = 8, K = 3;
Тест №3(задача B.3): A = 7, B = 11, C = 14, K = 5;
Тест №4(задача B.4): A = 12, B = 18, C = 25, K = 6;
Тест №5(задача B.5): A = 13, B = 19, C = 36, K = 7;
Тест №6(задача B.6): A = 15, B = 10, C = 16, K = 9;
Тест №7(задача B.7): A = 18, B = 26, C = 34, K = 10;
Тест №8(задача B.8): A = 5, B = 18, C = 41, K = 13;
Тест №9(задача B.9): A = 34, B = 21, C = 58, K = 16;
Тест №10(задача B.10): A = 789, B = 963, C = 1523, K = 51.
(3): (Всероссийская Олимпиада Школьников по информатике школьный уровень Московская область — 7-8 класс):(телепорт)
Вчера на день рождения Максиму подарили телепорт (устройство для телепортации). Сегодня Максим хочет опробовать его по дороге в школу.
Улицу, на которой живет Максим, можно представить в виде координатной прямой, на которой дом Максима имеет координату A метров, школа B метров, а скорость передвижения Максима равна 1 м/c. Телепорт открывает портал в определенной точке C на координатной прямой и при входе в него моментально перемещает Максима в определенную точку D на координатной прямой. Максим хочет как можно быстрее оказаться в школе. Максиму не обязательно использовать телепорт, но он может это сделать, если это ускоряет путь.
Определите по заданным числам A, B, C и D, через какое наименьшее количество секунд Максим сможет оказаться в школе.
Формат выходных данных.
Введите одно целое число — минимальное количество секунд, через которое Максим сможет попасть из дома в школу.
Замечание
Если, например, A = 2; B = 13; C = 4; D = 8, схематично можно изобразить расположение дома, телепорта и школы следующим образом:

Тогда Максиму выгодно пройти через телепорт, и он окажется в школе уже через t = C — A + B — D = 4 2 + 13 8 = 7 секунд.
Тест №1(задача А.1): A = 9, B = 18, C = 8, D = 17;
Тест №2(задача А.2): A = 7, B = 17, C = 11, D = 32;
Тест №3(задача А.3): A = 6, B = 21, C = 7, D = 40;
Тест №4(задача А.4): A = 6, B = 53, C = 51, D = 75;
Тест №5(задача А.5): A = 3, B = 19, C = 1, D = 50;
Тест №6(задача А.6): A = 13, B = 32, C = 27, D = 40;
Тест №7(задача А.7): A = 15, B = 27, C = 10, D = 27;
Тест №8(задача А.8): A = 30, B = 47, C = 20, D = 50;
Тест №9(задача А.9): A = 100, B = 235, C = 250, D = 281;
Тест №10(задача А.10): A = 183, B = 698, C = 345, D = 862.
(4): (Всероссийская Олимпиада Школьников по информатике школьный уровень Московская область — 9-11 класс):(новый офис)
Одна крупная компания открывает новый большой офис. Как известно, открытие офиса связано с большим количеством трудностей. Системный администратор Олег решает задачу предоставления сотрудникам проводного доступа в интернет.
У Олега есть бесконечное количество проводов, но, к сожалению, в новом офисе есть только один разъём от провайдера для подключения интернета. Однако в распоряжении Олега имеется несколько разветвителей. Разветвитель имеет один входной разъём и от одного до трех выходных разъёмов. В разъем от провайдера можно подключить или один компьютер или входной разъем одного разветвителя. В каждый выходной разъем разветвителя может быть подключен или один компьютер или другой разветвитель. Количество разветвителей в цепи подключений не ограничено. Всего в офисе есть N компьютеров, которые необходимо подключить к интернету. В распоряжении Олега имеется A разветвителей с одним выходным разъёмом, B разветвителей с двумя выходными разъёмами и C разветвителей с тремя выходными разъёмами.
Напишите программу, определяющую максимальное число компьютеров в офисе, к которым можно провести проводной интернет.
Формат входных данных
В первой строке вводится натуральное число N (1 <= N <=100) количество компьютеров в новом офисе.
Во второй строке вводится натуральное число A (1 <= A <= 100) количество разветвителей с одним выходным разъёмом.
В третьей строке вводится натуральное число B (1<= B <=100) количество разветвителей с двумя выходными разъёмами.
В четвёртой строке вводится натуральное число C (1<= C <= 100) количество разветвителей с тремя выходным разъёмами.
Формат выходных данных
Необходимо вывести одно натуральное число – максимальное количество компьютеров, к которым можно подвести проводной доступ в интернет.
Примеры:
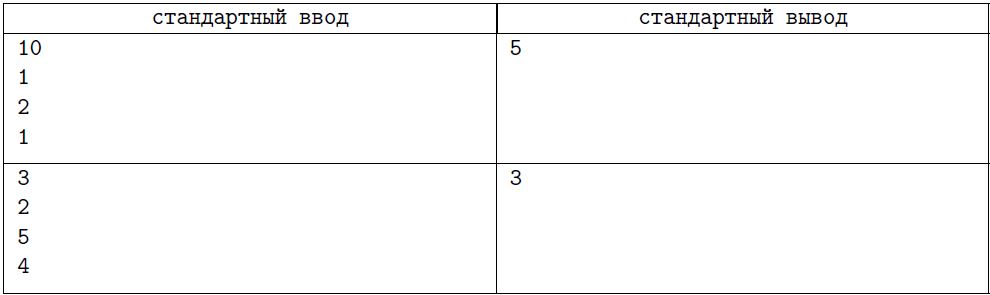
Замечания:
В первом примере в офисе всего 10 компьютеров. У Олега есть один разветвитель с одним выходным разъёмом, два разветвителя с двумя выходными разъёмами и один разветвитель с тремя. Олег может подключить разветвитель с тремя выходными разъёмами к разъёму от провайдера интернета в офисе. Далее к этому разветвителю можно подключить все остальные разветвители. Таким образом, максимально можно подключить к интернету 5 компьютеров.
Во втором примере ко всем трем компьютерам можно предоставить доступ в интернет.
(5): (Всероссийская Олимпиада Школьников по информатике школьный уровень Московская область — 9-11 класс):(Игра)
Петя и Маша решили сыграть в игру. Изначально у Пети и Маши N и M яблок соответственно. Первым ходом Петя передает одно яблоко Маше. На второй ход Маша отдает Пете 2 яблока. Далее Петя передает Маше 3 яблока, и игра продолжается до тех пор, пока у одного из игроков не заканчиваются яблоки. Формально, на шаге i + 1 получатель яблок из шага i передает второму игроку число яблок, равное переданному числу яблок на шаге i и еще одно.
Напишите программу, которая по заданным N и M вычислит через сколько шагов игра Пети и Маши закончится.
Формат входных данных
В первой строке подается число N (1<= N <=106) — начальное число яблок у Пети.
Во второй строке подается число M (1<= N <= 106) начальное число яблок у Маши.
Формат выходных данных
Выведите одно число количество ходов, через которое закончится игра.
Примеры:

Замечания:
В первом примере игра закончится после того, как Петя передаст 1 яблоко Маше и у него останется 0 яблок.
Во втором примере рассмотрим последовательность ходов: После первого хода: у Пети – 1 яблоко, у Маши 4. После второго: у Пети 3 яблока, у Маши 2.
После третьего: у Пети 0 яблок, у Маши – 5.
Игра на этом заканчивается, так как у Пети больше не осталось яблок.
(6): (Всероссийская Олимпиада Школьников по информатике муниципальный уровень Московская область — 7-8 класс):(Доски)
Иван – профессиональный строитель. Помимо тщательного контроля при строительстве он также следит за качеством материалов. Иван решил сделать деревянный забор, поэтому он приобрёл доску длиной L сантиметров. Однако для строительства забора необходимы доски длиной ровно D сантиметров. Разумеется доску можно распилить на несколько частей, но из-за сжатых сроков Иван успеет распилить её не более, чем на K частей. Ему стало интересно, какое максимальное количество досок длины D ему удастся получить? Напишите программу, которая по числам L, D, K вычисляет это количество.
Формат входных данных
В первой строке вводится натуральное число L (1 <= L <= 100) длина исходной доски.
Во второй строке вводится натуральное число D (1 <= D <= 100) требуемая длина досок.
В третьей строке вводится натуральное число K (2 <= K <= 100) максимальное количество частей, на которое можно распилить доску.
Формат выходных данных
Выведите единственное целое число – максимальное количество досок длины D, которое удастся получить.
Примеры:

Замечание:
В первом примере доску длины 10 можно распилить на 5 частей длины 2.
Во втором примере доску длины 11 можно распилить на 3 части длины 3 и одну часть длины 2.
В третьем примере разрешено распилить доску только на две части, поэтому пусть первая часть будет длины 3, а вторая часть длины 8.
(7): (Всероссийская Олимпиада Школьников по информатике муниципальный уровень Московская область — 9-11 класс):(Счастливые числа)
Федя совсем недавно поступил в лучший вуз страны. В особенности ему стала интересна кафедра изучения счастливых чисел, то есть тех чисел, которые состоят только из цифр 2 и 5. Научные сотрудники этой кафедры исследуют их распределение. Они поняли, что существует последовательность всех счастливых чисел в порядке возрастания (2 — первое число, 5 — второе, 22 — третье и т.д.). Они хотят найти порядковый номер счастливого числа N в данной последовательности. Федю очень заинтересовала эта задача. Он думал над ней целый день, но так ни к чему и не пришел. Можете ли вы помочь Феде и кафедре счастливых чисел найти ответ?
Формат входных данных
Тест №1: N = 25;
Тест №2: N = 55;
Тест №3: N = 225;
Тест №4: N = 5555;
Тест №5: N = 5522;
Тест №6: N = 255255525;
Тест №7: N = 555222255525252252;
Тест №8: N = 252252552252522555552525252222;
Тест №9: N = 255522222225522252255255222555552225222252555222222255252222;
Тест №10: N = 552222552555225252222555555522522555225255525252552222525255:
Формат выходных данных
Для каждого теста требуется ввести в тестирующую систему одно целое число порядковый номер счастливого числа N в последовательности счастливых чисел.
Замечание
Т.к. счастливое число 2 является первым числом последовательности счастливых чисел, то ответ на задачу при N = 2 равен 1. При N = 22, ответ равен 3. А например, т.к. число 255 является 10-ым членом последовательности, то при N = 255 ответ будет равен 10.
(8): (Всероссийская Олимпиада Школьников по информатике муниципальный уровень Московская область — 9-11 класс):(Тортики и свечки)
Сегодня знаменательный день! В Межгалактическом Обществе Программистов сразу у n программистов день рождения! Поскольку программисты в этом обществе – очень дружный народ, они решили отпраздновать эти дни рождения все вместе. Как известно, все разумные существа во вселенной в день рождения зажигают свечки на торте. Программисты зажигают свечки в соответствии с двоичной записью числа. Например, если программисту исполнилось 24 года, он втыкает в торт 5 свечек и зажигает только первые 2, поскольку 2410 = 110002, a если ему исполнилось 31, то придется зажечь все 5 свечек. Программисты быстро заметили, что если свечка не была зажжена то ее можно вытащить из торта и воткнуть в следующий. Конечно, они не хотят расходовать лишних свечек и поэтому решили посчитать, в каком порядке стоит праздновать дни рождения, чтобы минимизировать их расход. Поскольку общество межгалактическое, в нем есть индивиды самого разного возраста от 1 до 109 лет.
Напишите программу, которая определяет наименьшее количество свечек, которое потребуется, чтобы отпраздновать все дни рождения.
Формат входных данных
В первой строке находится одно число n (1 <= n <=100) – количество программистов.
Во второй строке находится n чисел ai (1 <= ai <= 109) – сколько лет исполняется каждому программисту.
Формат выходных данных
В первой строке выведите одно целое число – минимальное количество свечек, которое потребуется, чтобы отпраздновать все дни рождения.
Система оценки
Гарантируется, что решение, работающее, когда числа уже даны в правильном порядке наберет не менее 10 баллов.
Гарантируется, что решение, работающее, когда все числа имеют одинаковую длину в двоичной записи наберет не менее 30 баллов.
Примеры:

(9): (Всероссийская Олимпиада Школьников по информатике муниципальный уровень Московская область — 9-11 класс):(Системы счисления)
Сегодня Егор в школе проходил системы счисления, ему дали следующее определение представление числа в системе счисления:
Представлением целого положительного числа n в k-ичной системе счисления (k > 2) называется последовательность целых неотрицательных чисел a1, …, as такая, что ai <= k — 1 для всех i = 1…s, a1 не равное 0, а также as + as-1 * k + as-2 * k2 + … + a1 * ks-1 = n. Например, представлением числа 6 в двоичной системе счисления является последовательность 1; 1; 0, т.к. 0 + 1 2 + 1 4 = 6, а представлением числа 120 в одиннадцатиричной системе счисления является последовательность 10; 10, т.к. 10 + 10 11 = 120. Можно показать, что любое целое положительное число n представимо единственным образом в k-ичной системе счисления для любого k > 2. Егор считает красивыми последовательности, которые заканчиваются ровно на два нуля. Сего-дня в учебнике он наткнулся на целое положительное число n, и он захотел получить из него как можно больше красивых последовательностей, переводя n в различные системы счисления. Ему стало интересно, сколько различных красивых последовательностей он сможет получить? Однако, так как число n очень большое, без программирования ему не обойтись. К сожалению, программировать он не умеет, поэтому обратился за помощью к вам. Напишите программу, которая по заданному n считает количество различных красивых последовательностей, которые из него можно получить.
Формат входных данных
В единственной строке входных данных находится единственное целое число n (1 <= n <= 1018) – число, которое увидел Егор, идя из школы.
Обращаем внимание, что входные данные в этой задаче могут не поместиться в 32-битный целочисленный тип данных вашего языка, рекомендуется использовать 64-битный тип данных (long long, int64_t языка С++, int64 языка Free Pascal, long языка Java и т.д.)
Формат выходных данных
Выведите единственное число – ответ на задачу.
Система оценки
Решения, работающие корректно при n <= 106, будут оцениваться в 30 баллов.
Решения, работающие корректно при n <= 1012, будут оцениваться в 60 баллов.

Замечание
В первом тесте единственные системы счисления, в которых у числа 8 есть нули на конце – двоичная и четверичная, но в двоичной оно заканчивается на 3 нуля, а в четверичной на 1, так что ни та, ни другая не подходит.
Во втором тесте можно получить последовательность 1; 1; 0; 0, переведя 12 в двоичную систему счисления.
В третьем тесте можно получить последовательность 1; 1; 0; 0; 1; 0; 0, переведя 100 в двоичную систему счисления, последовательность 4; 0; 0, переведя 100 в пятиричную систему счисления и по-следовательность 1; 0; 0, переведя 100 в десятичную систему счисления. Обратите внимание, что 101-ричная система счисления не подходит для числа 100, т.к. 100 представляется в 101-ричной системе счисления как последовательность из одного числа 100, последний элемент этой последовательности равен 100, а не 0.
(10): (Всероссийская Олимпиада Школьников по информатике школьный уровень Московская область — 9-11 класс): (Автобусы)
Эта задача с открытыми тестами. Ее решением является набор ответов, а не про-грамма на языке программирования. Тесты указаны в самом условии, от вас требуется лишь ввести ответы на них в тестирующую систему.
Вадим добирается до места проведения олимпиады по информатике на автобусе. Он пришел на остановку в H часов и M минут. Все автобусы в его городе начинают движение с этой остановки в 8:00, а последний автобус проезжает через неё не позднее 22:00. Ему подходят автобусы двух типов: автобусы первого типа проходят через остановку Вадима каждые A минут, второго каждые B минут. Вадим, конечно, очень торопится, поэтому, когда автобус приходит, он сразу же в него садится. Если автобус приходит одновременно с Вадимом, то он тоже успевает в него сесть. Помогите Вадиму выяснить, какое минимальное количество минут ему придётся ждать.
Формат входных данных
Первая строка входных данных содержит целое число H (0 <= H <= 23). Вторая строка вход-ных данных содержит целое число M (0 <= M <= 59). Третья строка входных данных содержит целое число A (1 <= A <= 14*60 + 1). Четвертая строка входных данных содержит целое число B (1 <= B <=14*60+1).
Формат выходных данных
Если в этот день Вадим дождётся автобуса, требуется вывести одно целое число минимальное количество минут, которое ему придётся ждать. Иначе требуется вывести число “-1” (без кавычек).
Примеры
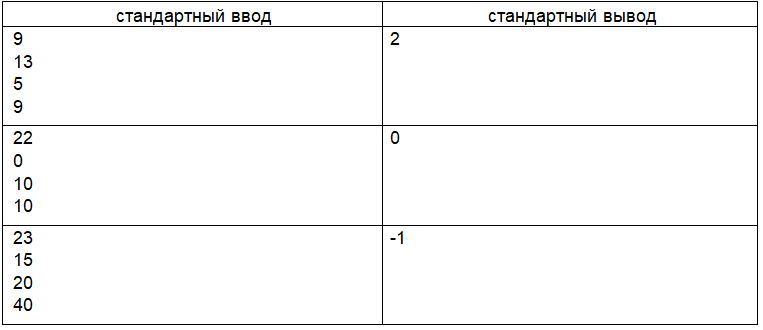
Замечание
В первом примере Вадим сядет на автобус первого типа, который придёт в 9:15, поэтому ждать ему придётся 2 минуты. Во втором примере Вадиму доступны автобусы обоих типов, которые в 22:00 будут на его остановке, поэтому ждать не придётся. В третьем примере Вадим не успеет ни на один автобус.
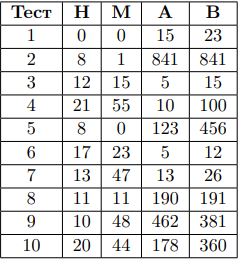
Тесты:
(11): (Всероссийская Олимпиада Школьников по информатике школьный уровень Московская область — 9-11 класс): (Фишки)
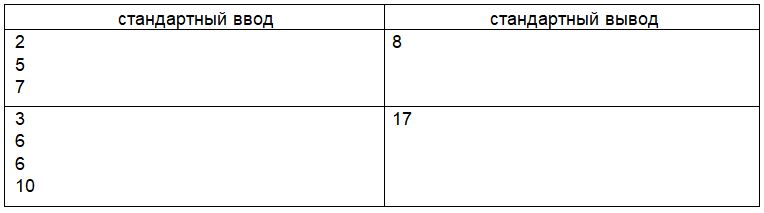
Вадим почти готов к началу своего путешествия от дома до места проведения олимпиады по информатике. На каждую олимпиаду Вадим берет с собой фишки, которые, по его мнению, приносят ему удачу. Каждая из этих фишек окрашена в один из k цветов. Фишек i-го цвета у Вадима ni штук. Вадим хочет решить все задачи олимпиады, поэтому сегодня ему нужны с собой фишки всех цветов. Все фишки хранятся в одной коробке, из которой Вадим достает их не глядя. Помогите ему понять, какое наименьшее количество фишек ему придётся достать, чтобы гарантированно вытащить фишки всех цветов?
Формат входных данных
В первой строке входных данных дано целое число k (1 <= k <= 106) количество цветов. Далее в k строках записаны числа n1; … nk (1 <= ni <= 103) количества фишек 1, … k цвета соответственно.
Формат выходных данных
Выведите одно целое число — наименьшее количество фишек, которое нужно достать, чтобы гарантированно получить фишки всех цветов.
Примеры:
(12): (Всероссийская Олимпиада Школьников по информатике школьный уровень Московская область — 9-11 класс): (Вдохновение)
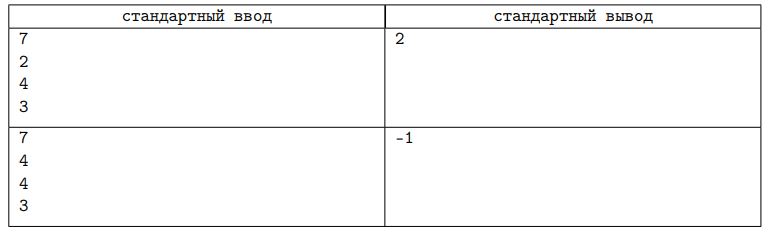
Программирование занятие творческое и тоже требует вдохновения! Вадим, подводя итоги последних нескольких дней, поделился с вами своими наблюдениями. Дни Вадима отличаются друг от друга наличием вдохновения. Вадим считает, что в течение дня у него может быть вдохновение для решения алгоритмических задач, вдохновение для написания промышленного кода или вдохновение для того и другого. Дни, когда вдохновение присутствует и для того, и для другого, называются продуктивными, поскольку именно тогда Вадим больше всего преуспевает в разработке своих проектов. В некоторые дни вдохновения может не быть совсем, ни для алгоритмов, ни для промышленного кода это не страшно, даже Вадиму иногда нужно отдыхать и отвлекаться от программирования! Назовем такие дни днями отдыха.
Вадим поделился с вами статистикой за n дней, а именно, вам известно, что a дней были продуктивными, b дней Вадим испытывал вдохновение для решения алгоритмических задач, c дней Вадим испытывал вдохновение для написания промышленного кода. Теперь вам стало интересно, какое количество дней отдыха было среди этих n дней? В случае, если Вадим ошибся, и такие числа n; a; b; c не могли получиться при подсчете, вам нужно сообщить об этом.
Формат входных данных
Вводятся четыре целых неотрицательных числа n; a; b; c (0 <= n; a; b; c <= 108), по одному в каждой строке. n обозначает суммарное количество дней, о которых Вадим делится статистикой, a количество продуктивных дней, b количество дней, когда Вадим испытывал вдохновение для решения алгоритмических задач, c количество дней, когда он испытывал вдохновение для написания промышленного кода.
Формат выходных данных
Выведите единственное число количество дней отдыха среди n дней. В случае, если Вадим ошибся, и данные числа n; a; b; c не могли получиться, выведите число 1. Гарантируется, что если ответ на задачу существует, то он единственный.
Примеры:
Замечание
В первом примере из условия Вадим делится с вами наблюдениями за неделю. Например, у него могло быть подходящее настроение для алгоритмических задач 4 дня с понедельника по четверг, а для промышленного программирования 3 дня со среды по пятницу. Тогда среда и четверг были продуктивными днями, а суббота и воскресенье днями отдыха. Поэтому ответ на этот тест равен 2. Во втором примере из условия данные числа n; a; b; c не могли получиться, поэтому ответом является специальное число — 1.
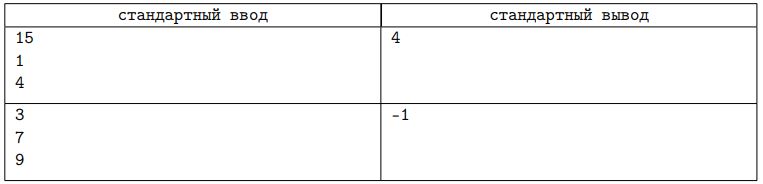
(13): (Всероссийская Олимпиада Школьников по информатике школьный уровень Московская область — 9-11 класс): (Аудитории)
Вадим добрался до места проведения олимпиады по информатике, где имеются аудитории со всеми номерами от 1 до n. Теперь среди них надо найти аудиторию, в которой проводится олимпиада. Из-за волнения Вадим забыл её номер, но что-то он всё-таки помнит номер нужной аудитории состоит только из цифр x и y в любом количестве (возможно, в номере встречается только одна цифра из этих двух, также x и y могут совпадать). Вадим собирается заходить в аудитории, номер которых может подойти, и спрашивать, не в них ли проводится олимпиада по информатике. Помогите Вадиму понять, какое наибольшее количество аудиторий ему придётся проверить, чтобы найти ту, в которой проводится олимпиада.
Формат входных данных
В первой строке входных данных записано целое число n (1 <= n <= 106) — количество аудиторий. Во второй строке записано целое число x (0 <= x <= 9) — первая цифра, которую запомнил Вадим. В третьей строке записано целое число y (0 <= y <= 9) — вторая цифра, которую запомнил Вадим.
Формат выходных данных
Если среди номеров аудиторий есть состоящие из цифр x и y, необходимо вывести одно целое число — наибольшее количество аудиторий, которое Вадиму придётся проверить. Если таких номеров нет, необходимо вывести число “-1” (без кавычек).
Примеры:
Замечание
В первом примере среди номеров от 1 до 15 есть четыре номера, состоящих только из цифр 1 и 4, — это 1; 4; 11; 14. Во втором примере среди номеров 1; 2; 3 нет номеров, состоящих только из цифр
7 и 9.
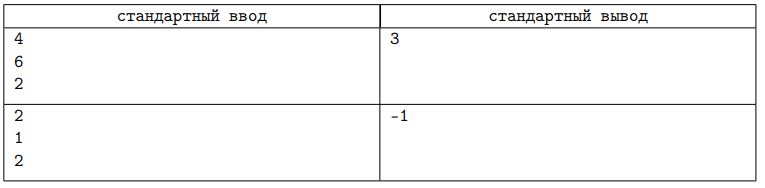
(14): (Всероссийская Олимпиада Школьников по информатике муниципальный уровень Московская область — 9-11 класс) : (Поддержание бодрости)
Игорь начинает готовиться к олимпиаде, которая состоится через N дней. Игорь готовится к олимпиаде по вечерам, после того, как возвращается из школы и делает всю домашнюю работу. Каждый вечер Игорь может либо учиться, либо лечь спать пораньше. Если Игорь сегодня ложится спать пораньше, его уровень бодрости повышается на A единиц, если учится снижается на B единиц. Игорь хочет составить себе расписание на каждый день для каждого дня выбрать, будет ли он учиться или ляжет спать пораньше. При этом Игорь хочет составить расписание на N дней таким образом, чтобы учиться как можно больше дней, а его уровень бодрости через N дней должен быть таким же, как и сейчас.
Определите, сможет ли Игорь составить себе такое расписание, и, если сможет, вычислите, сколь-ко дней Игорь будет учиться. Считается, что уровень бодрости может быть отрицательным.
Формат входных данных
В первой строке вводится натуральное число N (1 <= N <= 1018) количество дней до олимпиады.
Во второй строке вводится натуральное число A (1 <= A <= 1018) число единиц, на которое повышается бодрость Игоря за каждый день, когда он выбирает лечь спать пораньше.
В третьей строке вводится натуральное число B (1 <= B <= 1018) число единиц, на которое понижается бодрость Игоря за каждый день, когда он выбирает учиться.
Гарантируется, что N * A <= 1018
Формат выходных данных
Если Игорь не сможет составить себе расписание, удовлетворяющее условиям, выведите -1. Если Игорь сможет составить себе расписание, удовлетворяющее условиям, выведите количество дней учебы в этом расписании.
Система оценки
Гарантируется, что решения, работающие корректно при n <= 105, будут получать не менее 50 баллов.
Примеры
Замечание
В первом примере из условия Игорь может учиться 3 дня, а отдыхать один. За каждый день уче-бы его бодрость уменьшается на 2, то есть всего уменьшается на 6, а за день отдыха увеличивается на 6. Таким образом, его уровень бодрости через 4 дня останется таким же.
Во втором примере из условия если Игорь один день отдыхает, а второй учится, его уровень бодрости сначала увеличится на 1, а потом уменьшится на 2. Таким образом, через 2 дня он будет на 1 меньше, чем был изначально. В случае, если Игорь будет 2 дня учится, его уровень бодрости уменьшится на 4, а если будет 2 дня отдыхать, его уровень бодрости увеличится на 2. Таким образом, не существует сценария, при котором его уровень бодрости не изменится за 2 дня. Поэтому, в этом примере ответ на задачу -1.
(15): (Всероссийская Олимпиада Школьников по информатике муниципальный уровень Московская область — 9-11 класс) : (История о ферматисте)
Эта задача с открытыми тестами. Ее решением является набор ответов, а не про-грамма на языке программирования. Тесты указаны в самом условии, от вас требуется лишь ввести ответы на них в тестирующую систему.
Однажды всемирно известный Доцент, вновь доказывая Великую теорему Ферма, обнаружил удивительное свойство! Взяв 4 различных простых числа A; B; C; D, он заметил, что произведение A * B и произведение C * D дают одинаковые остатки от деления на некоторое натуральное число K. Как настоящий Доцент, он решил узнать, при каком максимальном K может выполняться такое равенство. К сожалению, сейчас Доцент слишком занят доказательством теоремы Ферма, поэтому он поручил эту задачу Вам.
Формат входных данных
Формат выходных данных
Выведите единственное число максимальное K, при котором выполняется равенство.
Система оценки
Каждый тест оценивается независимо в 10 баллов.
Замечание
Рассмотрим пример, при котором A = 3; B = 5; C = 11; D = 2.
A * B = 15, C * D = 22. Тогда можно заметить, что при K > 22 остатки от деления на K не будут меняться и будут различны. Легко убедиться, что для K <= 22 максимальное значение, при котором выполняется нужное равенство, будет K = 7.
(16): (Всероссийская Олимпиада Школьников по информатике муниципальный уровень Московская область — 9-11 класс) : (Ресторанный бизнес)
Эта задача с открытым тестированием. Решения по этой задаче тестируются в открытую, во время олимпиады. Вы можете не дожидаться окончания олимпиады, чтобы узнать итоговый балл вашего решения по этой задаче.
Как известно, Тимур лучший поставщик продуктов во всей Московской области. В Московской области существует всего n ресторанов, в c из которых Тимур уже поставляет продукты. Также, m пар ресторанов являются соседями друг для друга, при этом ресторан не может быть соседом сам себе и никакие два ресторана не могут быть соседями дважды.
Так как Тимур не разбирается в рекламе, то новости о его качественной работе распространяются только с помощью сарафанного радио, а именно ресторан решает нанять Тимура как поставщика, если хотя бы в k соседей этого ресторана Тимур уже поставляет продукты.
Тимур очень дальновидный, поэтому его интересует, какие из ресторанов однажды наймут его как поставщика. Но так как сейчас он занят развозом товара, он поручил эту непростую задачу Вам!
Формат входных данных
Первая строка содержит три целых числа n; m; k (1 <= k <= n <= 2*105, 1 <= m <= min((n*(n-1))/2, 2*105)), обозначающее количество ресторанов, количество пар соседей и количество соседей, необходимое для того, чтобы ресторан нанял Тимура, соответственно.
В следующих m строчках содержится описание пар соседних ресторанов. Каждая строка содержит два различных целых числа ui; vi номера двух ресторанов, соседних друг другу (1 <= ui; vi <= n; ui != vi). Гарантируется что одна и та же пара не встречается в этом списке дважды.
В следующей строке содержится целое число c (0 <= c <= n), обозначающее количество ресторанов, в которые Тимур с самого начала поставляет продукты.
В следующей строке содержится c различных целых чисел от 1 до n номера ресторанов, в которые Тимур уже поставляет продукты.
Формат выходных данных
В первой строке выведите целое число a количество ресторанов, которые однажды наймут Тимура как поставщика.
Во второй строке выведите a целых чисел номера всех ресторанов, в которые Тимур будет поставлять продукты, в любом порядке.
Система оценки
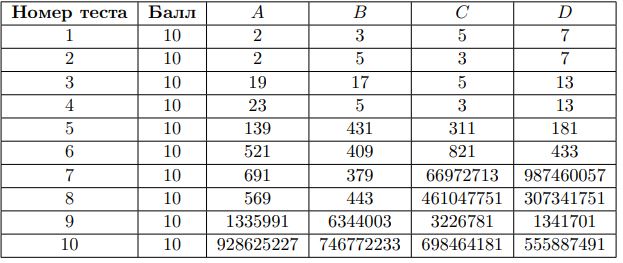
Тесты к этой задаче состоят из шести групп. Баллы за каждую группу ставятся при прохождении всех тестов этой группы, а также при прохождении тестов необходимых подгрупп. Баллы за соответствующие группы указаны в таблице.

Пример

Замечание
Пояснение к тесту из условия выглядит следующим образом:

Изначально только в три ресторана с номерами 1, 2 и 5 Тимур поставляет продукты. После этого ресторан с номером 3 также решает нанять Тимура, ведь у него есть двое соседей, в которые Тимур уже поставляет продукты. Далее ресторан под номером 4 тоже решает нанять Тимура, ведь его соседи с номерами 3 и 5 уже работают с Тимуром. Таким образом, все 5 ресторанов будут сотрудничать с Тимуром.
(17): (Всероссийская Олимпиада Школьников по информатике муниципальный уровень Московская область — 9-11 класс) : (Мега OR)
Эта задача с открытым тестированием. Решения по этой задаче тестируются в открытую, во время олимпиады. Вы можете не дожидаться окончания олимпиады, чтобы узнать итоговый балл вашего решения по этой задаче.
Однажды Саше попалась последовательность a, состоящая из 109 целых неотрицательных чисел. Ему известны значения первых n элементов последовательности, остальные элементы равны нулю. Саша любит битовые операции и структуры данных, поэтому он решил дать Вам следующую задачу: необходимо выполнить q запросов. Запросы бывают двух типов:
1) i v — заменить элемент с индексом i на число v, т.е. присвоить ai = v.
2) z — вычислить количество целых неотрицательных чисел x, таких что (a1 or a2 or … or a10^9 or x) <= z
Напишите программу, которая сможет обработать эти запросы достаточно быстро.
Формат входных данных
В первой строке входных данных содержится одно целое число n (1 <= n <= 100 000) — количество первых элементов массива a, которые знает Саша.
Во второй строке содержится n целых чисел a1, a2, … an (0 <= ai <= 230 — 1).
В третьей строке входных данных содержится одно целое число q (1 <= q <= 100 000) — количество запросов.
Следующие q строк описывают запросы. В каждой из них находится числo t (1 <= t <= 2) — тип запроса.
Если t = 1, то в строке содержатся еще два целых числа i и v (1 <= i <= 109, 0 <= v <= 230 -1).
Если t = 2, то в строке содержится еще одно целое число z (0 <= z <= 230-1).
Формат выходных данных
Для каждого запроса второго типа в отдельной строке выведите ответ на запрос.
Система оценки
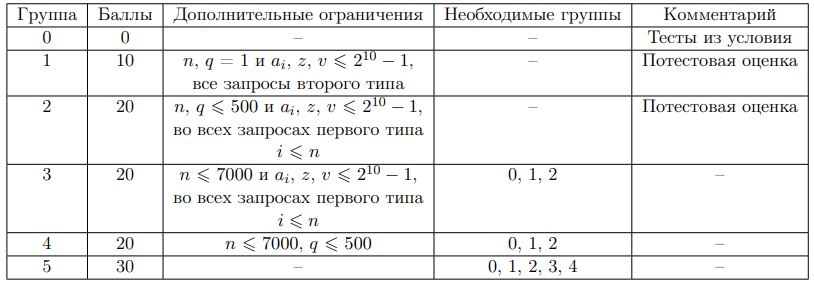
Тесты к этой задаче состоят из шести групп. Баллы за каждую группу ставятся при прохождении всех тестов этой группы, а также при прохождении тестов необходимых подгрупп. Баллы за соответствующие группы указаны в таблице. Исключение составляют группы 1 и 2, которые оцениваются за каждый пройденный тест отдельно.
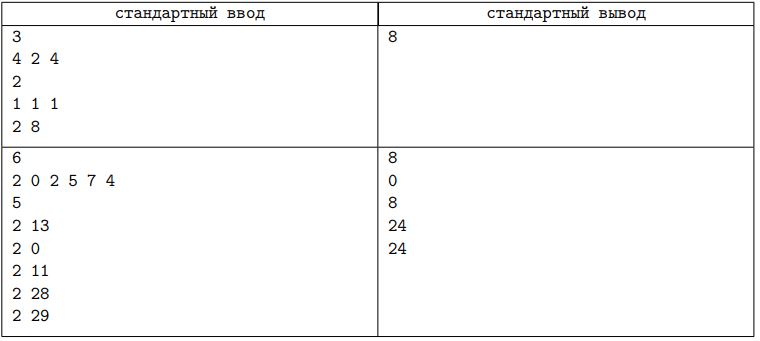
Примеры
Замечание
Операция or обозначает операцию побитового «ИЛИ».
Побитовое «ИЛИ» бинарная операция, действие которой эквивалентно применению логического «ИЛИ» к каждой паре битов, которые стоят на одинаковых позициях в двоичных представлениях операндов. Другими словами, если оба соответствующих бита операндов равны 0, двоичный разряд результата равен 0, иначе двоичный разряд результата равен 1.
Разберем первый пример из условия. Изначально дана последовательность [4; 2; 4], после первого запроса a1 = 1 последовательность становится [1; 2; 4]. Поступает второй запрос z = 8. Можно убедиться, что для всех x от 0 до 7 выполняется (1 or 2 or 4 or x) <= 8, а для всех x > 7 выполняется (1 or 2 or 4 or x) > 8. Поэтому ответ на второй запрос равен 8.
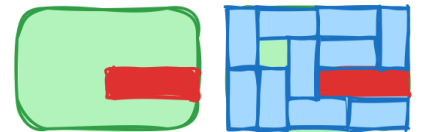
(18): (Всероссийская Олимпиада Школьников по информатике школьный уровень Московская область — 9-11 класс): (Прямоугольник без центра)
Вам дали клетчатый прямоугольник размерами n на m клеток. Вам очень захотелось крутить его на пальце, а для этого нужно прорезать в его середине дырку.
Определим центр прямоугольника как точку пересечения его диагоналей. Из прямоугольника нужно вырезать все клетки, для которых центр прямоугольника находится внутри или на границе (в том числе в углу клетки).
После вырезания центра вам нужно будет покрасить оставшиеся клетки. Известно, что на 1 клетку расходуется 1 мл краски. Сколько краски потребуется?
Формат входных данных
На вход даются два целых числа: n; m — размеры прямоугольника (4 <= n; m <= 104).
Формат выходных данных
Выведите одно целое число — требуемое количество миллилитров краски.
Примеры

Замечание
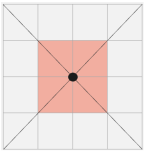
Иллюстрация для n = m = 4
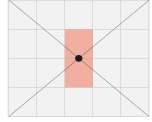
Иллюстрация для n = 4; m = 5
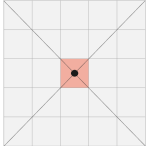
Иллюстрация для n = m = 5
(19): (Всероссийская Олимпиада Школьников по информатике школьный уровень Московская область — 9-11 класс): (Викторина)
Эта задача с открытыми тестами. Ее решением является набор ответов, а не программа на языке программирования. Тесты указаны в самом условии, от вас требуется лишь ввести ответы на них в тестирующую систему.
Викторина состоит из пяти вопросов стоимостью 10; 20; 30; 40; 50 очков. Вопросы задаются последовательно, на каждый вопрос участник может попытаться дать ответ либо не отвечать. Если участник решил не отвечать, то он не получает очков. Если же участник решил дать ответ, то в случае правильного ответа к его результату игры прибавляется стоимость вопроса, в случае неправильного ответа из результата игры вычитается стоимость вопроса. Например, если участник правильно ответил на вопросы за 10 и 20, затем решил не отвечать на вопросы за 30 и 40, и наконец ответил неверно на вопрос за 50, то его результат игры равен
10+20 — 50= — 20.
Вам известно, что участник ответил верно на x вопросов и неверно на y (гарантируется, что x+y <= 5). На оставшиеся вопросы участник решил не отвечать. Найдите все возможные результаты игры, которые могли получиться, и упорядочите их по возрастанию.
Формат входных данных
Вводится два целых числа x; y (0 <= x; y <= 5; x+ y <= 5) количество вопросов, на которые участник ответил верно, и количество вопросов, на которые участник ответил неверно, соответственно.
Формат выходных данных
Выведите все возможные результаты игры в возрастающем порядке через пробел.
Система оценки
Каждый тест, кроме примеров из условия, оценивается независимо в 10 баллов.
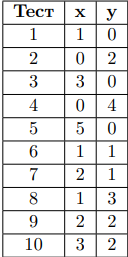
Примеры

Замечание
В первом примере из условия известно, что участник ответил на четыре вопроса верно и на один неверно. Соответственно, есть 5 вариантов:
10 + 20 + 30 + 40 — 50 = 50
10 + 20 + 30 — 40 + 50 = 70
10 + 20 — 30 + 40 + 50 = 90
10 — 20 + 30 + 40 + 50 = 110
-10 + 20 + 30 + 40 + 50 = 130
Во втором примере из условия участник просто решил не отвечать ни на один вопрос, поэтому результат игры может быть только нулем.
(20): (Всероссийская Олимпиада Школьников по информатике школьный уровень Московская область — 9-11 класс): (Новые парковочные места)
Гипермаркет «КодингВилл» скоро откроет свои двери для всех своих клиентов! Однако ему до сих пор кое-чего не хватает — хорошей парковки. Поэтому вас наняли, чтобы сделать самую удобную и просторную парковку на n машин. Сама парковка делится на несколько блоков по два столбика, все эти блоки расположены в один ряд вдоль магазина так, чтобы машины были припаркованы параллельно стене. Пример такого блока можно увидеть на картинке.
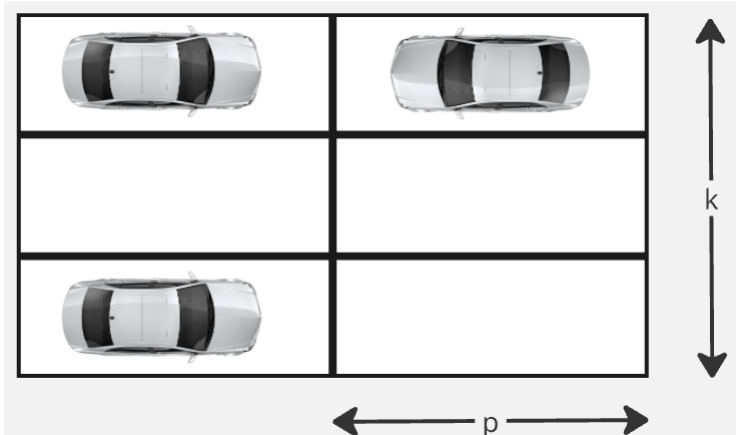
В техническом задании указана следующая информация о том, что должна представлять из себя парковка:
- Вместимость должна быть не менее n автомобилей.
- Каждый из двух столбиков отдельного блока должен вмещать в себя k автомобилей.
- Длина главной стены гипермаркета — L метров.
- Длина парковочного места должна быть p метров. Толщиной линии, разделяющей парковочные места, можно пренебречь.
Ваша цель — опираясь на данное техническое задание, максимизировать расстояние между блоками парковки. При этом оно должно быть одинаковым между блоками, а сами блоки не должны выходить за пределы главной стены гипермаркета. А чтобы проектировать было проще, ответ должен быть целым числом.
Формат входных данных
Вводится четыре целых числа n, k, l , p (1 <= n, k, l, p <= 109) количество автомобилей, вместимость одного столбика блока парковки, длина главной стены магазина, длина одного парковочного места.
Формат выходных данных
Выведите единственное целое число — максимальное расстояние между блоками. Если достаточно только одного парковочного блока , или парковку вовсе невозможно построить по заданным параметрам, выведите -1.
Примеры

Замечание
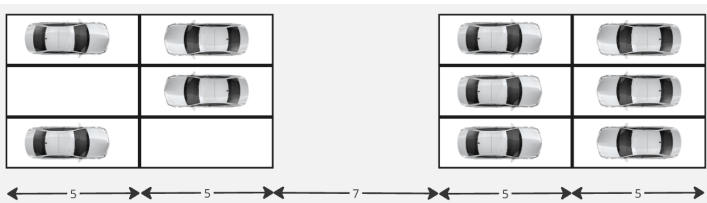
Иллюстрация для первого примера из условия
(21): (Всероссийская Олимпиада Школьников по информатике школьный уровень Московская область — 9-11 класс): (Домино и домино)
Домино всегда мог постоять за себя, и за его длинную жизнь он добился возможности охотиться на огромном пространстве, которое для простоты мы будем считать ровным полем, состоящим из n на m клеток. И сейчас пришло время разделить это поле на охотничьи угодья для своих детей. Домино считает, что для начала каждому ребенку будет достаточно выделить по 2 клетки. Но при этом Домино хочет избежать конфликтов между детьми, поэтому он хочет, чтобы для каждого ребенка его две клетки имели общую сторону. К сожалению, главный враг Домино – мама-лань всё ещё живёт неподалеку от него. Её ореол обитания мы также упростим до прямоугольника. Чтобы задать этот прямоугольник, мы пронумеруем строки и столбцы охотничьих угодий Домино от 1 до n и от 1 до m соответственно. Тогда ореол обитания мамы-лани задаётся координатами x1; y1 и x2; y2 верхнего левого и правого нижнего углов соответственно. При этом гарантируется, что охотничьи угодьи Домино составляют связную область. Домино волнуется, что его угодий не хватит для всех его детей, поэтому просит Вас посчитать, какое максимальное количество охотничьих условий для детей сможет выделить Домино из своего поля, не затрагивая ореол обитания мамы-лани.
Формат входных данных
В первой строке входных данных даны два целых числа n; m(1 <= n; m <= 109) – размеры охотничьих угодий Домино. Во второй строке входных данных даны 4 целых числа: x1; y1; x2; y2(1 <= x1 <= x2 <= n; 1 <= y1 <= y2 <= m) – координаты левого верхнего и правого нижнего углов прямоугольника, в котором обитает лань.
Формат выходных данных
Выведите одно число – максимальное количество детей, которым Домино сможет выделить кусочек своего охотничьего угодья, состоящий из двух клеток с общей стороной.
Примеры

Замечание
В первом примере Домино может разделить поле между 10 детьми. Можно показать, что его охотничьи угодья нельзя разделить между большим числом детей, чтобы выполнить правила Домино. Разделение на 10 детей показано на следующей картинке: